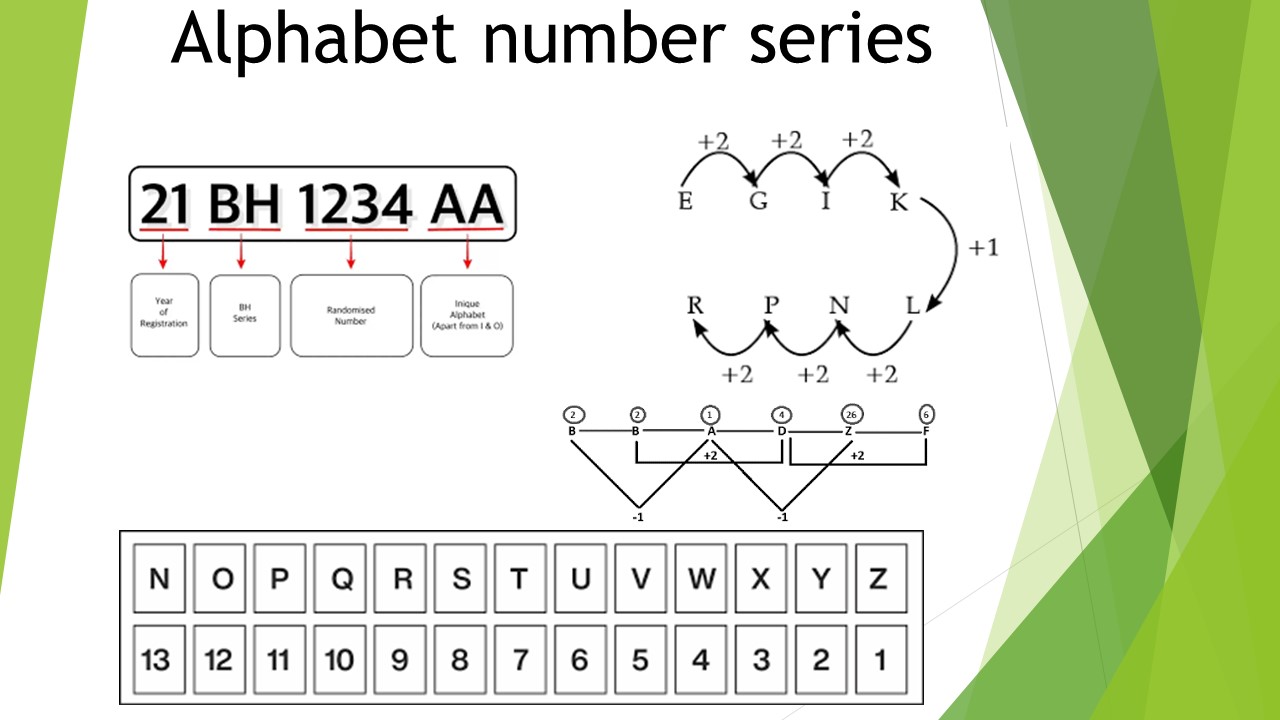
Alphabet number series
Sure! Here’s an example of an alphabet number series where each letter corresponds to its position in the English alphabet:
| Letter | Position (Number) |
|---|---|
| A | 1 |
| B | 2 |
| C | 3 |
| D | 4 |
| E | 5 |
| F | 6 |
| G | 7 |
| H | 8 |
| I | 9 |
| J | 10 |
| K | 11 |
| L | 12 |
| M | 13 |
| N | 14 |
| O | 15 |
| P | 16 |
| Q | 17 |
| R | 18 |
| S | 19 |
| T | 20 |
| U | 21 |
| V | 22 |
| W | 23 |
| X | 24 |
| Y | 25 |
| Z | 26 |
If you want, I can create a specific series, like a coded message, or an example where letters alternate with numbers.
Here’s a clear explanation of the logical concept behind an alphabet number series:
An alphabet number series assigns a numerical value to each letter based on its position in the alphabet, starting with A = 1, B = 2, and so on up to Z = 26. This concept allows us to convert letters into numbers, making it easier to analyze patterns, create codes, or solve puzzles involving sequences of letters.
The logic behind this is simple and sequential: the English alphabet has 26 letters arranged in a fixed order. By numbering them from 1 to 26, we create a consistent system to reference each letter numerically. This system is widely used in cryptography, coding, and learning tools because numbers are easier to manipulate mathematically than letters.
For example, the word “CAT” can be represented as the number series 3-1-20, corresponding to C=3, A=1, T=20. This numeric representation can be used to create patterns or perform arithmetic operations, like adding or subtracting values to generate new codes or sequences.
Sure! Here’s an example question using the alphabet number series concept:
Example Question:
Using the alphabet number series where A = 1, B = 2, C = 3, and so on, find the sum of the letters in the word “SPACE”.
Step-by-step:
- S = 19
- P = 16
- A = 1
- C = 3
- E = 5
Sum: 19 + 16 + 1 + 3 + 5 = 44
Great question! There are several types of alphabet number series used in logical reasoning, coding, puzzles, and aptitude tests. Here’s a breakdown of the most common types:
1. Direct Letter-to-Number Mapping
Each letter is replaced by its corresponding alphabetical position:
- A = 1, B = 2, …, Z = 26
Example: “DOG” → D=4, O=15, G=7 → 4, 15, 7
2. Reverse Alphabet Series
The letters are mapped in reverse:
- A = 26, B = 25, …, Z = 1
Example: “CAT” → C=24, A=26, T=7 → 24, 26, 7
3. Arithmetic Series Using Letters
Patterns are based on the alphabetical positions increasing/decreasing by a constant difference.
Example: A, C, E, G → Positions: 1, 3, 5, 7 → +2 each time
Find the next letter: I (9)
4. Letter Shifting (Caesar Cipher Style)
Each letter is shifted forward or backward by a fixed number.
Example: Shift each letter in “HELLO” by +2 →
H → J, E → G, L → N, L → N, O → Q → “JGNNQ”
5. Mixed Series (Alternating Patterns)
Combines letters and numbers in alternating or patterned ways.
Example: A1, C3, E5, G7 → Letters move by +2, Numbers by +2
Next: I9
6. Positional Code Series
Involves using the position of the letter in a word or a sentence to determine the code.
Example: In the word “WORLD”, each letter might be encoded as:
W (4th in alphabet from the end = 4), O (12), R (9), L (15), D (23)
Absolutely! Here are more advanced and creative types of alphabet number series used in logical reasoning and puzzles:
7. Double Letter Number Series
Uses the sum or difference of positions of two letters in a pair.
Example:
Series: AB (1+2=3), CD (3+4=7), EF (5+6=11), GH (7+8=15)
Pattern: Sum increases by +4 each time
Next pair: IJ (9+10 = 19)
8. Odd-Even Letter Series
Letters are selected based on odd or even positions in the alphabet.
- Odd letters: A=1, C=3, E=5…
- Even letters: B=2, D=4, F=6…
Example: Series: A, C, E, G → All odd-positioned letters
Next letter: I (9)
9. Fibonacci-Based Letter Series
Use Fibonacci logic with letter positions.
Example:
A = 1, B = 2, C = 3 (1+2), E = 5 (2+3), H = 8 (3+5), M = 13 (5+8)
Follow Fibonacci with letter positions: A, B, C, E, H, M…
🪄 10. Vowel-Consonant Pattern Series
Patterns alternate or follow sequences based on vowels/consonants.
Example: A, C, E, G, I → Alternating vowel-consonant-vowel…
Next: K
11. Decreasing Letter Series
Letters decrease by a constant step.
Example: Z, X, V, T → Positions: 26, 24, 22, 20 → Step -2
Next: R (18)
12. Zigzag or Non-linear Series
The pattern jumps forward and backward.
Example: A, D, B, E, C, F → Forward +3, then back -2, repeat
Next: D, G
13. Target-Based Series
Find a hidden letter based on a goal number.
Example: Find a letter such that the sum of two letters = 20
If A=1, and the first letter is C (3), the second must be N (17)
Would you like practice questions or puzzles based on any of these? I can also generate a mini quiz!
Here’s a concise and effective conclusion for a topic on Alphabet Number Series and Logical Concepts:
Conclusion:
Alphabet number series offer a fascinating way to connect language with logic and mathematics. By assigning numerical values to letters and identifying patterns, we can unlock a wide variety of puzzles and reasoning exercises that sharpen problem-solving skills. Whether it’s direct letter-to-number conversions, shifting patterns, or complex coded sequences, these series help develop logical thinking, attention to detail, and analytical ability. Understanding the different types and techniques behind these patterns not only improves performance in competitive exams and brain games but also enhances overall cognitive flexibility.



